Implementierung II: Operationen und Berechnungen

Eine Kasse besteht neben der Eingabe über Scanner oder Tasten und der Ausgabe in Form eines Displays aus einer Recheneinheit, und verschiedenen Geldfächern. Ein- und Ausgabe sollen zunächst vernachlässigt werden, weil sie Teil der späteren Benutzerschnittstelle sind. Damit bleibt zum einen als Eigenschaft der Kasse bestehen, dass sie verschiedene Geldfächer enthält. Zum anderen muss die Kasse verschiedene Rechenoperationen ausführen können, um dem Kassierer die Arbeit zu erleichtern. Die Kasse sollte:

Beträge summieren können,
die Bezahlung einlagern,
das nötige Wechselgeld errechnen können,
prüfen können, ob genug Wechselgeld vorhanden ist, und
das Wechselgeld bereitstellen.

Jeder der Forderungen steht eine Fähigkeit, also eine Methode der Klasse KASSE gegenüber:

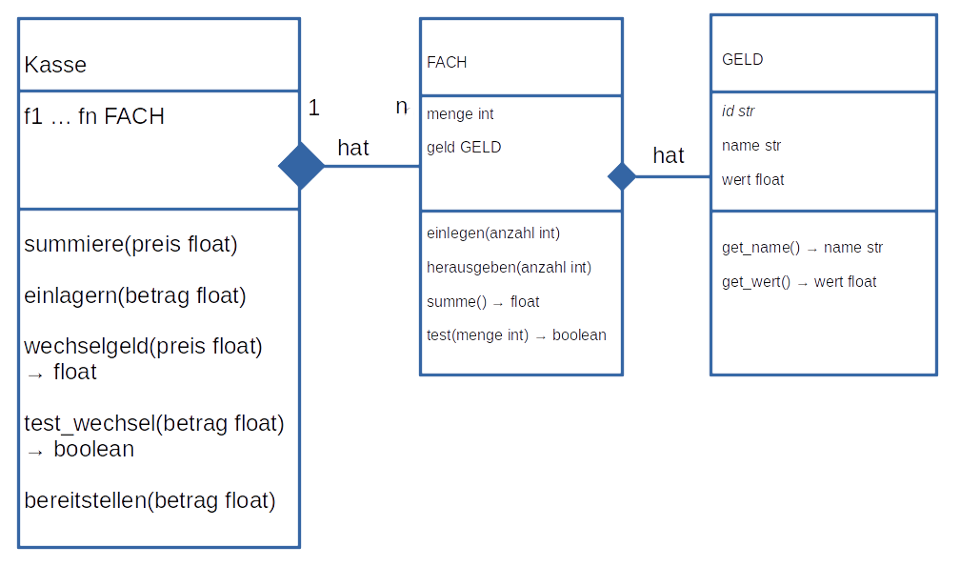
Abb. 5: Klassendiagramm KASSE hat FACH hat GELD

A) Der Testfall

In einem Testfall soll die Kasse mit einer Menge an Wechselgeld gestartet werden. Anschließend werden Werte summiert und der Gesamtwert überprüft. Die Menge an Geld eines Faches wird abgefragt, bevor man einen bestimmten Geldbetrag einlagert; danach wird die Menge im Fach nochmals überprüft. Die Funktion test() müsste dann aufgerufen mit einer größeren Anzahl als Geldeinheiten im Fach sind False ergeben und bei einer geringeren Anzahl True. Schließlich sollte bereitstellen() die richtige Stückelung an Geldeinheiten zu einem Kommabetrag enthalten und die Menge der Geldeinheiten in einem bestimmten Fach um die richtige Anzahl reduzieren.

B) Grundlagen der nötigen Rechenoperationen

Die Methoden summiere(float betrag) und wechselgeld(float betrag) bestehen aus einer Addition bzw. einer Subtraktion von Kommawerten. Die Methoden einlagern(float betrag), test_wechsel(float betrag) und bereitstellen(float betrag) beruhen dagegen auf dem Berechnen der Anzahl von Geldeinheiten, die in einem Kommabetrag enthalten sind. So muss etwa bereitstellen(float betrag) abbilden, aus wie vielen unterschiedlichen Geldenheiten sich der Kommawert zusammensetzt.

Ganzzahlige Division int(a/b)

Wenn man mit Geldeinheiten rechnet, muss das Ergebnis einer Division immer ganzzahlig sein, weil eine Einheit entweder noch enthalten ist oder eben nicht mehr. So ist in 2,20 € genau ein 2 € Stück enthalten, aber nicht 2,2 Eurostücke. Das Ergebnis der Divison 2,20€ / 2€ muss also ein ganzzahliges Ergebnis liefern, also int(2,20/2).

Modulo (%)

Der Restbetrag der ganzzahligen Division ergibt sich am einfachsten durch eine Modulo-Operation. So ergeben 2,20 modulo 2 ebenso wie 4,20 % 2 die gewünschten 0,20, also genau den Restbetrag, der übrig bleibt, wenn man die nötige Anzahl an 2 Euromünzen bereits in Empfang genommen oder herausgegeben hat.

C) Berechung am Beispiel von test_wechsel(float betrag)

Der folgende Programmablaufplan stellt die nötigen Arbeitsschritte zum Überprüfen der Menge an Wechselgeld und ihren Zusammenhang dar.

Abb. 7: Ablauf in der Methode test(float betrag) -> boolean

def test(self, betrag):
# Wissen: return beendet die Ausführung einer Funktion
    # für jedes Geldfach tue
    for f in self.ReiheDerFaecher:
        # benötigte Stückzahl =
        #  ganzzahlige Division von 
        #  Betrag durch Wert des Geldes im Fach   
       menge = int(betrag / f.geld.get_wert())
        # Überprüfe ob die Sückzahl im Fach ist: 
        #              Nein? Gib zurück False       
       if not f.test(menge): return False
       # Neuer Betrag = Restbetrag 
       #     <= Betrag modulo Geldwert            
       betrag = round(betrag % f.geld.get_wert(), 2) 
    return True
    # Alle Fächer durchlaufen ohne Abbruch? 
    # Gib zurück True

Aufgabe:

Programmiere die fehlenden Methoden aus, so dass das Skript fehlerfrei abläuft und richtig funktioniert.

Weiter: Implementierung III: Steuerung und Interface >>