Kategorie: Informatik 10 – 1. Teil
07 Viele bewegte Kreise
Bewegung am Bildschirm ist immer eine Frage der zugrunde liegenden Graphikbibliothek. Die Turtle erlaubt es aber in gewissem Rahmen Animationen mit mehreren Objekten ablaufen zu lassen. Dazu soll die neue Klasse ANIMKREIS verwendet werden.
Die Vorlage zum Programmieren findest Du hier: prg07_vielbewegung.
Bewegung erfolgt am Bildschirm von einer Position (x1;y1) zu einer Position (x2;y2). Ein kleinster Schritt wäre eine Verschiebung um dx = 1 und dy = 1, also z.B. von Position (2;3) zu Position (3;4). Das wäre eine Bewegung im 45°-Winkel um etwa ein Pixel nach rechts oben. Ein größerer Schritt wäre zum Beispiel eine Verschiebung um dx = 5 und dy = 5, also z.B. von Position (2;3) zu Position (7;8). Dem entspräche eine Bewegung im 45°-Winkel um etwa sieben Pixel (Pythagoras) nach rechts oben.
Aufgabe 1
Ein zusätzliche Attribut speed der Klasse ANIMKREIS soll Werte zwischen (-12,-12) und (12,12) annehmen können. Dazu eignet sich ein so genannter „Setter“, eine Methode, die geeignete Werte als Parameter entgegen nimmt und ein bestimmtes Attribut der Klasse mit diesen Werten belegt.
def set_speed(self, ...): self.speed = ...
Probiere es aus.
Exkurs: Hilfreiche Zufallszahlen
Hin und wieder sind Zufallszahlen sehr praktisch, zum Beispiel wenn Geschwindigkeitsvektoren zufällig gesetzt werden sollen. Dazu importiert man das Modul random und kann anschließend verschiedene Funktionen des Moduls aufrufen.
import random
a = random.randint(0,12) # eine Ganzzahl zwischen 0 und 12
print('a: '+str(a))
b = random.random() # eine Kommazahl zwischen 0 und 1
print('b: '+str(b))
c = random.randint(-12,12) # eine Ganzzahl zwischen -12 und 12
print('c: '+str(c))
Aufgabe 2
Die Bewegung des Kreises soll nicht bei jedem Aufruf von außen bestimmt werden, sondern in Abhängigkeit von dem Attribut speed mit seinen Komponenten dx und dy erfolgen:
def bewege(self): self.loesche() dx, dy = self.speed self.update(dx, dy) self.zeichne()
Aufgabe 3
Im Hauptprogramms sollen 5 Kreise an der Position (0;0) erzeugt werden, die alle jeweils andere, zufällige Geschwindigkeiten haben. Eine Schleife soll diese Kreise anschließend 100 mal jeweils um einen Schritt weiterbewegen.
Nächstes Kapitel: Ende der ersten Einheit
06 Etwas Bewegung
Die Stärke der Objektorientierung liegt zweitens in der Möglichkeit durch „Vererbung“ existierende Klassen wiederzuverwenden und dabei nach Bedarf anzupassen.
Beispiel: Aus KREIS wird ANIMKREIS.
Ziel: Objekte der Klasse Kreis sollen von Position 1 nach Position 2 bewegt werden können.
Frage 1: Wie bewegt man eine Figur im Bild?
Antwort: Man kann eine Figur zeichnen, sie dann an der aktuellen Stelle löschen, und dann den Kreis mit geänderten Positionswerte neu zeichnen.
Frage 2: Wie löscht man eine Figur?
Antwort: In dem man die Figur mit der Farbe des Hintergrunds – z.B. ‚white‘ – an derselben Stelle nochmals zeichnet.
Frage 3: Wie zeichnet man die Figur mit geänderten Positionswerten?
Antwort: Erst die Positionswerte ändern, dann zeichnen.
Frage 4: Wie ändert man die Positonswerte?
Antwort:
x,y = self.position # Immer rechts vom = nach links lesen! x = x + dx y = y + dy self.position = (x, y)

Aufgabe:
Implementiere die Methoden loesche() und bewege() in der vorbereiteten Klasse ANIMKREIS: prg06_bewegung.
Nächstes Kapitel: 07 Viele bewegte Kreise
05 Vererbung
Objektorientierten Programmcode kann man durch Vererbung wiederverwenden. Durch „Vererbung“ kann man bestehende Eigenschaften und Methoden einer Klasse nutzen, man kann sie aber auch ergänzen oder abwandeln.
Beispiel:
Die Klasse RECHTECK kann man verwenden um eine Klasse QUADRAT zu bauen. Das Quadrat ist dem Rechteck ja sehr ähnlich: Je zwei parallele Seiten, vier rechte Winkel. Aber beim Quadrat sind eben alle Seiten gleich lang.

Vererbung im Codebeispiel
import turtle, geomfig
class QUADRAT(geomfig.RECHTECK): # In dieser Zeile findet die
# Vererbung statt.
def __init__(self, pos, s, col): # Nur der Konstruktor wird
# geändert.
self.position = pos
self.weite = s # Weite <- Parameter Seitenlänge
self.hoehe = s # Höhe <- Parameter Seitenlänge
self.color = col
# Der Rest bleibt gleich.
#------- Testprogramm --------------#
if __name__ =="__main__":
q = QUADRAT( (10,10), 30, 'red' )
q.zeichne()
Probiere es aus: prg05_vererbung
Aufgabe
- Schreibe eine Klasse GDREIECK für gleichseitige Dreiecke.
Verwende dazu durch Vererbung soviel Code der Klasse DREIECK wie möglich. - Betrachte alltägliche Dinge, die uns umgeben. Was davon könnte man mit dem Konzept der Vererbung beschreiben? Zum Beispiel ‚Fahrzeuge‘?
Vielleicht fallen Dir auch noch andere Beispiele ein.
Nächstes Kapitel: 06 Etwas Bewegung
04 Funktionsgraphen mit Kreisen zeichnen
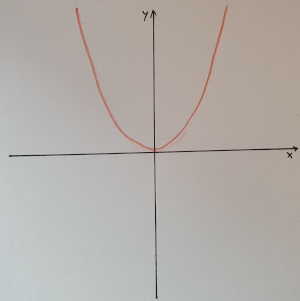
Kleine Kreise nimmt das Auge als Punkte wahr. Mit vielen kleine Kreisen kann man daher auch Geraden oder Parabeln zeichnen.
Aufgabe 1
a) Ändere das Programm 04 so, dass das untenstehende Bild gezeichnet wird.

b) Ergänze Programm 04 um ein Koordinatensystem. Beachte, dass das Koordinatensystem zuerst gezeichnet wird und erst danach der Funktionsgraph. Vielleicht findest dazu das Modul koordinaten.py hilfreich.
Aufgabe 2
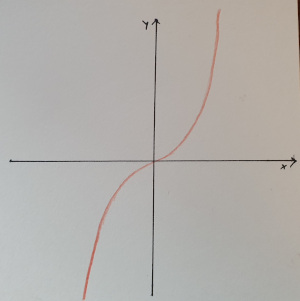
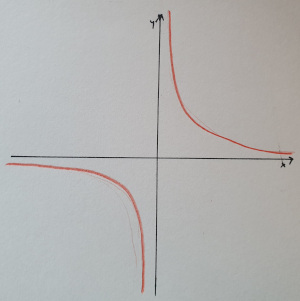
Versuche mit dem Programm die folgenden Ausgaben zu produzieren.
Hyperbeln sind etwas schwieriger, weil die Stelle n = 0 berücksichtigt werden muss.
Nächstes Kapitel: 05 Vererbung
03 Vier Kreise
Die Stärke der Objektorientierung liegt zum einen in der Skalierbarkeit: Wer einen Kreis zeichnen kann, der kann auch 100 oder 1000 zeichnen lassen.
Für die folgenden Aufgaben sind schon ein paar Dateien vorbereitet, die man importieren kann: geomfig, koordinaten. Du findest die beiden Dateien im Archiv imports.zip. Verwende die Dateien lokal, indem Du sie herunterlädst, entpackst, kontrollierst und dann bei Bedarf importierst. Damit der Import funktioniert, müssen die zu importierenden Module im selben Verzeichnis liegen wie das aktuelle Skript, das Du programmierst.
In der Programmierumgebung Trinket.io findest Du die zu importierenden Dateien neben dem Hauptprogramm.

Aufgabe:
Ergänze das Hauptprogramm so, dass vier gleich große Kreise symmetrisch in den vier Sektoren gezeichnet werden. Dazu nehmen wir an, dass im Hintergrund des Screens ein Koordinatensystem liegt, das seinen Ursprung in der Mitte hat.
Nächstes Kapitel: 04 Funktionsgraphen mit Kreisen zeichnen
02 Weitere Formen
Neben dem Kreis lassen sich auch viele andere geometrische Formen relativ leicht mit der Python Turtle nachbauen.
Aufgabe 2.1:
Vervollständige zunächst die Klasse RECHTECK und teste sie.
Implementiere dazu die Methode zeichne().
Du brauchst dazu die Turtle-Methoden up(), down(), goto( position), forward(strecke), left(grad).
Aufgabe 2.2:
Vervollständige die Klasse DREIECK und teste sie.
Implementiere dazu den Konstruktor.
Nächstes Kapitel: 03 Vier Kreise
01 Einfache Objekte
Objekte sind Einheiten in Programmen, die Eigenschaften (Attribute) und Methoden haben. Einfache geometrische Formen lassen sich als Objekte auffassen und mit der Python-Turtle nachbauen.
Ein Kreis verfügt zum Beispiel über Eigenschaften wie Position, Radius und Farbe. Die Darstellung am Bildschirm erfordert eine Methode zeichne(). Eine Bauplan zur Herstellung von Kreisen müsste daher diese Eigenschaften und mindestens diese eine Methode haben.

Baupläne für Objekte heißen Klassen. Die Klasse KREIS ist durch ein UML-Diagramm rechts im Bild dargestellt.
Aufgabe 1:
a) Der Kreis soll mit Füllung gezeichnet werden. Beseitige dazu an zwei Stellen die Kommentarzeichen, sodass die Methode zeichne() den Kreis mit einer Farbe füllt.
b) Wandle das Programm so ab, dass der Kreis eine andere Farbe, eine andere Größe und eine andere Position bekommt.
Schlüsselwörter und Besonderheiten
class: Es leitet die Definition einer Klasse ein. Nach class folgt in allen Fällen der Name der Klasse, etwa KREIS, RECHTECK, DREIECK, usw. Klassennamen können frei gewählt werden, solange es nicht Schlüsselwörter sind. Am Ende der Zeile steht ein Doppelpunkt. Alles was zur aktuellen Klasse gehört, wird danach um einen festen Abstand eingerückt.
def: Um eine Funktion oder eine Methode zu definieren dient das Schlüsselwort def. Es folgen der Name der Funktion oder Methode, zwei Klammern und ein Doppelpunkt. Alles was zur aktuellen Definition gehört, wird danach um einen festen Abstand eingerückt.
self: Dieses Wort stellt einen Bezug innerhalb einer Klasse her her. Weil ein Name häufig nur in einem bestimmten Raum, in einem bestimmten Kontext eindeutig ist, bedeutet self soviel wie „dein eigene(r)“. Innerhalb einer Klassendefinition wird daher immer dann self geschrieben, wenn die „eigene“ Eigenschaft oder die „eigene“ Methode gemeint ist. Im oberen Beispiel etwa self.radius oder self.zeichne().
__init__: Dieses Wort bezeichnet die Konstruktormethode einer Klasse in Python. Der Konstruktor hat immer denselben Namen.
Nächstes Kapitel: 02 Geometrische Formen
Informatik 10
Objektorientierte Programmierung und Modellierung.
März 2020. Die folgenden Beiträge sind zur Unterstützung des Online-Unterrichts in Zeiten der Quarantäne gedacht. Ich gehe von meinem eigenen Unterricht aus. Wer anderes sieht und denkt, der kann gerne die Kommentarfunktion verwenden. Zusammen sieht man meistens mehr.
Als Programmiersprache zum Erlernen von objektorientierter Programmierung und Modellierung wird hier Python verwendet.
Python ist als Programmiersprache bis auf wenige Ausnahmen durchgehend objektorientiert aufgebaut. Ein Erkennungszeichen ist Dot-Syntax (Punktschreibweise). Module, Funktionen, Variablen … das sind alles Objekte.
Nächstes Kapitel: 01 Der Kreis